剪辑：剪辑部

【新智元导读】谷歌DeepMind的AI，终于拿下IMO金牌了！六个月前缺憾摘银，如今一举得金，SKEST新算法立大功。这不，它首破解了2009 IMO最难几何题，补助作图的神来之笔解法让谷歌扣问员赶紧战栗。

时隔6个多月，AlphaGeometry 2径直攻下IMO金牌！

刚刚，谷歌DeepMind一篇28页时间答复，公布了AG2最新冲破——

在2000-2024年IMO几何题上，解题率从54%飙升至84%。

论文地址：https://arxiv.org/pdf/2502.03544

畴前近25年IMO几何真题（50谈），AG2横扫了42谈。要知谈，这个成绩已经大幅超于积年IMO金牌得主的平均水平。

客岁7月，谷歌曾官宣的两大AI系统AlphaProof和AlphaGeometry 2，距离金牌只好1分之遥。

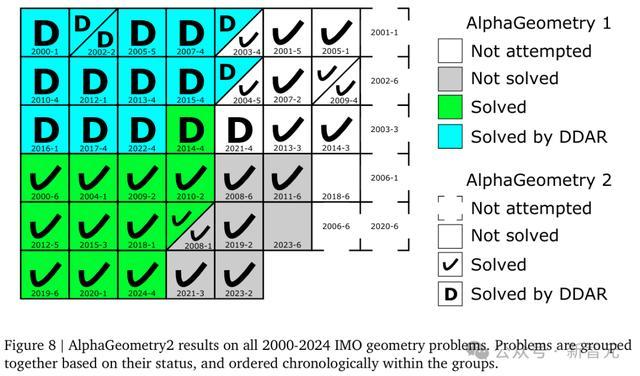
论文中，团队专为AG2联想了一种全新搜索算法——基于学问分享集成的搜索树（SKEST），允很多个集束搜索（beam search）并走时行并相互匡助。

成绩于这个算法，AG2好像在19秒内，搞定IMO 2024年P4题。

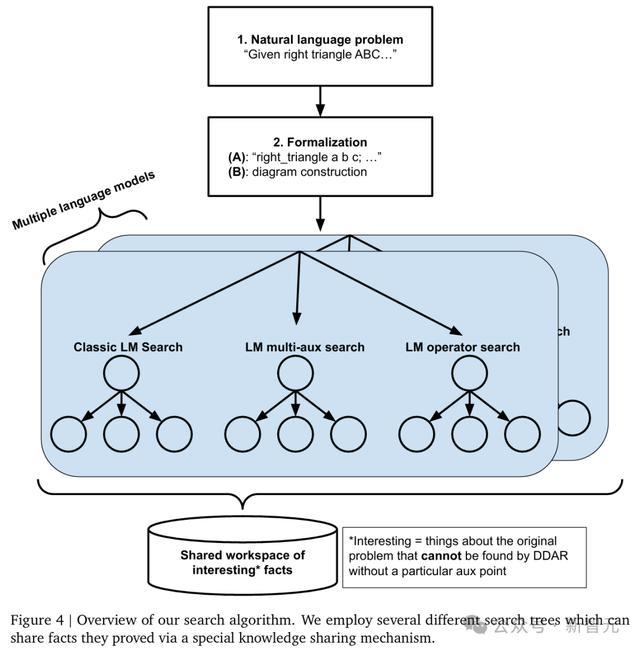
谷歌DeepMind高档扣问科学家Thang Luong称，「这是AI初次破解了2009年IMO最难几何题G7（备选题）」。

此前，这谈题只好贪图性解法（使用复数、三角贪图等）。

令东谈主诧异的是，AG2利用要道的补助作图（图中的红点），给出了一个只需要「角度」和「比例推导」的优雅解法。

这些点，是由神经象征架构中的「神经网罗模子」预计得出的。

有网友默示，「AGI似乎在谷歌里面杀青了」。

AG2，一举卓著IMO金牌得主

看成群众最具巨擘的高数竞赛，IMO几何题不仅练习选手对数学见解深远贯串，更需要极强的创造性想维。

而今天，数学这个东谈主类聪惠的结晶，正被东谈主工智能以惊东谈主的速率攻克。

第一代AlphaGeometry（AG1）通过将说话模子与象征引擎相聚拢，在畴前25年的IMO几何题中杀青了54%解题率。

在其时看来，这个成绩已是相配地惊东谈主。

AG1使用了肤浅特定域说话，主要由表1列出的九个基本的「谓词」构成

不外，AG1仍在几个要道范围存在局限性，比如特定说话范围、象征引擎效果，以及运转说话模子的才智均会影响其性能。

新一代AlphaGeometry 2，得到了全新升级。

它摄取了基于Gemini更雄伟的说话模子，其在更大更万般化数据聚拢完成历练，权贵擢升了贯串和推理才智。

同期，谷歌还引入了更快速、更持重的「象征引擎」，融入了简化礼貌集、增强双重心处理等优化。

此外，模子范围说话范围也进行了推广，涵盖了更往常的几何见解，包括轨迹定理和线性方程。

为了进一步擢升性能，团队还拓荒了一种新式搜索算法，探索更万般的补助作图战略，并摄取学问分享机制，来推广和加速搜索经过。

AG2最令东谈主凝视的进展之一是，统共自动化的处理才智。

它不错径直贯串当然说话体式的几何问题，借助Gemini团队的时间将问题回荡为专用说话，杀青了一种全新的「自动图形生成」算法。

成绩于以上的矫正，AG2在扫数IMO几何题上，取得了令东谈主印象深远的84%解题率。

这意味着，它已经卓著了IMO金牌得主的平均水平。

追想来说，AG2带来了几项首要升级：

推广了范围特定说话（DSL）的粉饰范围，可粉饰88%的IMO几何题目，比拟此前的66%有权贵擢升

矫正了象征引擎，使其愈加持重，且速率擢升了两个数目级

增强了说话模子，该模子基于Gemini并在更大限制（擢升一个数目级）和更万般化的数据集上历练

翻新性地提议了一种名为「基于学问分享集成的搜索树」（SKEST）的新算法，好像杀青多个搜索树之间的学问分享

更通用的域说话，粉饰88%题目

如上，表1列出的AG1九个基本「谓词」，已经粉饰了2000-2024年IMO几何题目中66%的问题。

然则，AG1的说话无法抒发线性方程、点/线/圆的移动，也无法处理「求角度...」这么的常见问题。

由此，谷歌扣问东谈主员在AG1的基础上，增多了两个「谓词」，不错搞定「查找X」类型的问题：

另外，在某些几何问题中，包括IMO 2024中的一起题目，存在AG1无法抒发的几何量（角度、距离）的线性方程。

为了抒发这些见解，AG2增多了以下三个谓词：

还有少量是，AG1不撑握所谓的「轨迹问题」，这类问题触及点、线和圆等对象的清醒，AG2则通过新的谓词语法捕捉这类问题。

表2列出了11种轨迹情况终点对应的谓词和语法。这里使用了一个新的象征*看成固定点的占位符。

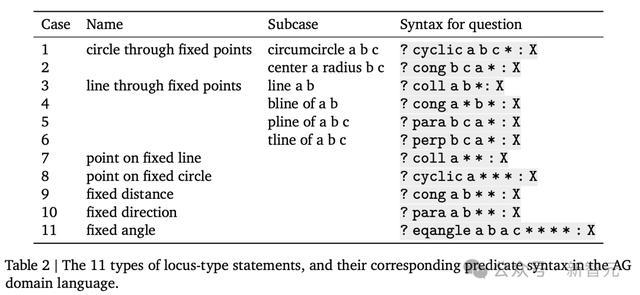
除此之外，AG2通过引入一个新的谓词 overlap a b（点A和点B是重合点）来施展点的非沉寂性，其中触及A的任何谓词也不错用于B，反之也是。

在推理闭包（deduction closure）经过中，重合点不错通过看成团结个圆的圆心来界说；

因此，团队引入另一个谓词cyclic_with_center来花样这种情况。因此，cyclic_with_center a1 a2 ... an x默示a_1=a_2=...=a_x是经过点a_x+1...a_n的圆的圆心（当x=0 时，等同于cyclic）。

自动体式化和图形生成

自动体式化

AG1以终点他访佛的神经象征系统有一个主要短处，需要手动将当然说话的输入改造成特定范围的说话。

举例，一个肤浅的当然说话几何问题「给定三角形ABC，其中双方非常AB=AC，施展角B和角C非常」，在AlphaGeometry的范围特定说话中变成了：「triangle a b c; a b = a c ? eqangle b a b c c b c a」。

在AG2中，团队率先通过东谈主工将几十个几何问题翻译成AG说话。然后，使用这些示例编写少样本领导，要求Gemini将给定的几何问题从当然说话翻译成AG说话。

用这个领导在Gemini中查询五次，然后再调用一次将这些截止合并成一个最终谜底。

通过这种范例，AG2好像将IMO 2000-2024中的39个几何问题体式化30个。对于肤浅的几何问题，这种范例非常灵验，险些莫得虚伪。

自动图形生成

对于无法径直通过几何作图构建的图形（非构造性问题），AG2摄取两阶段数值优化范例：

第一阶段使用ADAM梯度下跌优化，最小化瑕玷，同期防护点重合和坐标值过大。第二阶段使用Gauss-Newton-Levenberg（高斯-牛顿-勒文伯格）范例，求解非线性方程组，得到精准的图形坐标。

扣问团队在44谈IMO问题上进行了基准测试，经过上头的优化后，AG2好像为其中41个问题找到图形。

大多数问题在AG2第一次尝试时，以致几秒钟内就生成了图形。对于剩余的问题，也不错通过更长的运行时刻和更多的并行化运算获取图形。

举例，在使用了3333个程度运算了400分钟后，AG2获取了IMO-2011-6（2011年IMO第6题）的图形。

更雄伟、更快的象征引擎

AlphaGeometry2的中枢是「象征引擎」DDAR（演绎数据库与算术推理）。

这是一种用来贪图「演绎闭包」的算法。

所谓演绎闭包，便是从一堆最基本的已知县实动身，通过推理能得到的扫数事实的集聚。

DDAR有一套固定的推理礼貌，然后它会按照这些礼貌，一步阵势推导出新的事实，把新事实加到集聚里，直到没法再推出新的东西为止。

这使它能在两个方面发扬要道作用：一是为说话模子生成历练数据，二是在测试时进行施展搜索，寻找演绎尺度。

在这两种情况下，速率王人至关病笃。

更快的数据生成意味着不错进行更大限制、更透顶的数据过滤；而更快的施展搜索则意味着不错使得搜索更往常，从而增多了在给定时刻内找到搞定决策的可能性。

DDAR的三个主要矫正：处理重合点的才智（不错贯串为处理更复杂几何图形的才智）、更快的算法和更快的杀青。

处理重合点

在AG1中，若是两个点在几何上重合，但称呼不同，则系统无法识别它们是团结个点。举例，若是两条线a和b相交于点X，而咱们想施展X在某个圆ω上，AG1可能会难以处理这种情况。

AG2通过允许使用具有不同称呼但坐标相易的点来搞定这个问题。

这种处理重合点的才智非常病笃，因为它允许AG2通过「重新表述」来搞定问题。在某些情况下，径直施展某个点位于某个圆上可能很坚苦，但通过引入补助点并施展该补助点具有相易的性质，不错简化施展经过。

沟通一个施展两条直线a和b的交点X在圆ω上的例子。

AG2不错通过以下尺度杀青：率先，创建一个新的点 X'，该点是a和ω的交点；接下来，施展X'位于b上。由于X和X'王人位于a和b上，不错得出论断，X和X'是同少量，从而施展X位于ω上。

下图1直不雅地展示了上述施展经过。

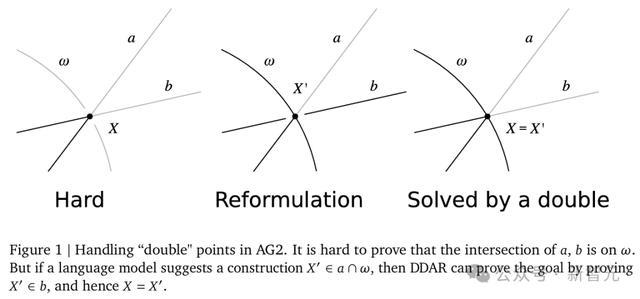
通过这些矫正，AG2不错更活泼地处理万般几何问题，况且好像以更接近东谈主类想维的样式搞定问题。

更快的算法

AG1的DDAR算法在处理礼貌列表时，会尝试将每条文定应用于扫数可能的点。

为了提高搜索效果，AG2径直硬编码了其应用搜索经过，从而减少了对AR子引擎的查询次数，最多查询三次。

AG2还丢弃了角度和距离的明确礼貌（举例对于垂直或平行线的礼貌），这些推导王人自动在AR引擎中进行。此外，AG2联想了一种矫正的DDAR2算法。

通过这些矫正，AG2权贵提高了搜索速率和效果，从而加速了施展经过，使得AG2好像更灵验地搞定复杂的几何问题。

更快的杀青

AG2的中枢贪图部分，额外是高斯消元法，使用C++重新杀青。为了与Python环境兼容，AG2使用pybind11将 C++库导出到Python。

通过C++重新杀青，AG2的速率比AG1快了300多倍。

这意味着AG2在相易的时刻内不错完成更多的贪图，从而更灵验地搞定复杂的几何问题。

更好的合成历练数据

AG2的顺利很大程度上归功于其矫正的合成历练数据。

AG2使用与AG1相易的尺度，但通过扩大资源和矫正算法，生成了更大、更万般化、更复杂的数据集，从而权贵擢升了模子的性能。

AG2率先立时采样几何图形，然后使用象征引擎（DDAR）推导出扫数可能的事实。对于每个推导出的事实，使用回溯算法提真金不怕火相应的前提、补助点和推导尺度。

AG2严格从立时图入手，这么不错摒除数据羞辱的风险，并探索可能超出东谈主类已知定理分袂的定理。

这种范例与TongGeometry等依赖东谈主类专科学问和现存问题图来领导和过滤数据生成的范例酿成了昭着对比。

更大、更复杂的图和更好的数据分袂

AG2探索的立时图大小是AG1的两倍，从而不错提真金不怕火更复杂的问题。

生成的定理在复杂性上提高了一倍，包括更多的点和前提。生成的施展尺度最多增多了10倍。

AG2在有和莫得补助点的施展之间有更均衡的数据分袂，比例接近50:50，而AG1中有补助点的施展比例仅为9%。

下图2展示了AG2比拟于AG1中包含了更多复杂、更长的问题，在每个问题类型中王人有更均衡的分袂。

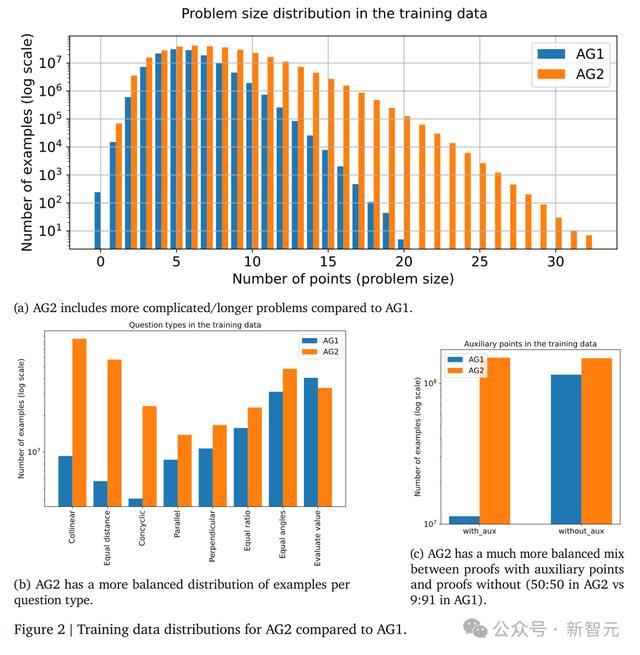
更多类型的定理

除了生成施展经典陈说（如「AB = CD」）的定理外，AG2的数据生成算法还生成「轨迹」类型的问题，举例 「当X在直线/圆Y上移动时，Z在固定直线/圆T上移动」。

AG2通过一个函数P(.)记载每个点在立时图生成经过中的清醒依赖性，从而撑握轨迹类型问题的生成。

下表3泄露了P(.)函数的两个示例，解释了若何笃定点的清醒源。

更快的数据生成算法

AG1率先在立时图上运行演绎闭包，然后「回溯」以获取最小问题和施展。

为了获取AG1中的最小问题，必须穷举地从问题中移除不同的点集，然后重新运行DDAR来检讨可施展性。这对于多数的点来说是不可行的

AG2改用了筹商丢弃算法，该算法只需进行线性次数的检讨，就不错判断一组点是否足以施展标的。只消检讨是单调的（若是A是B的子集，那么若是A可施展，则B也可施展），贪默算法保证能找到一个对于包含干系的最小点集。

新颖的搜索算法

在AG2中，扣问东谈主员联想了一种新颖的搜索算法——基于学问分享集成的搜索树（SKEST）。

在每棵搜索树中，一个节点对应于一次补助构造尝试以及随后的象征引擎运行。

若是该尝试顺利，扫数搜索诞生即远离。若是尝试失败，该节点会将象征引擎顺利施展的事实记载到分享事实数据库中。

经过筛选，这些分享事实不会包含节点本人私有的补助点，而只保留与原始问题猜想的践诺，以确保它们对团结搜索树中的其他节点以及不同搜索树中的节点王人具有价值。

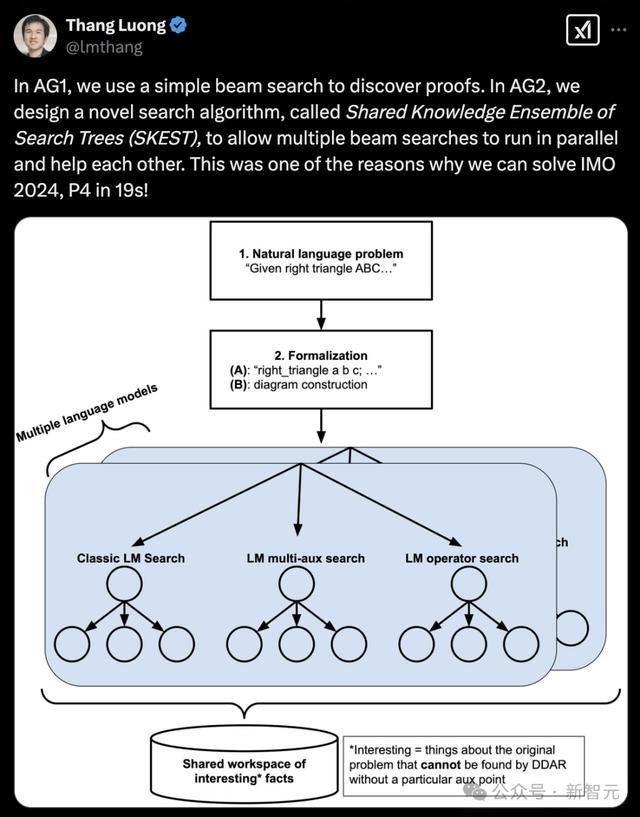
为了确保搜索空间的不同部分王人能得到灵验探索，扣问东谈主员摄取了以下几种搜索树：

「经典」搜索树：这种搜索树使用与AG1相易的集束搜索，其中说话模子在每个节点仅生成一个补助点。

在每个节点预计多个补助点的搜索树：说话模子被允许在每个树节点生成多个补助点。

这是可行的，因为说话模子经过历练，不错生成竣工的施展，从补助点入手，并按序推导出推理尺度。

尽管扣问东谈主员的标的是让模子在一次查询中生成扫数必要的补助点，但在实施中，他们发现频繁需要屡次调用模子，以利用先前生成的补助点。允许模子生成多个补助点好像加速求解经过，并灵验地增多搜索树的深度。

历练确立

AG1说话模子是一个自界说Transformer，在无监督模式下经过两个阶段的历练：率先在包含和不包含补助构造的题目上历练，然后仅在包含补助构造的题目上历练。

对于AG2，扣问东谈主员摄取Gemini历练活水线，并将历练简化为一个阶段，即在所额外据上进行无监督学习。

这个新说话模子是一个基于Gemini构建的MoE模子，并在AG2的数据集上历练。

扣问东谈主员历练了多种不同限制的模子，摄取三种历练决策：

1. 从零入手历练，使用范围特定说话（DSL）的自界说分词器（与AG1相易）。

2. 微调预历练的数学专用Gemini模子，使用当然说话进行历练。

3. 多模态历练，从零入手并额外引入图像输入，即几何题主见图示。

除了一个包含约3亿条定理的大型合成历练集，扣问东谈主员还构建了三个评估集：

1. 合成问题集「eval」：包含带有和不带有补助点的问题。

2. 合成问题集「eval_aux」：仅包含带有补助点的问题。

3. IMO评估集「imo_eval」：由2000-2024年IMO中，AlphaGeometry先前顺利搞定的几何问题构成。

扫数这些评估集王人包含竣工的施展，扣问东谈主员在历练经过上钩算它们的困惑度失掉。

与AG1相易，主要量度标的是IMO题主观点答率，其中说话模子生成补助点后，使用DDAR算法聚拢集束搜索进行求解。

扣问东谈主员使用TPUv4进行历练，并摄取最大可能的批大小，以充分利用硬件资源。学习率改造战略为线性预热（warm-up）+ 余弦退火（cosine anneal），其中学习率的超参数基于scaling laws设定。

图5展示了不同限制Gemini模子的学习弧线（以参数目为度量）。

如预期所示，模子限制越大，历练集、评估集以及IMO评估集的困惑度失掉均会镌汰。

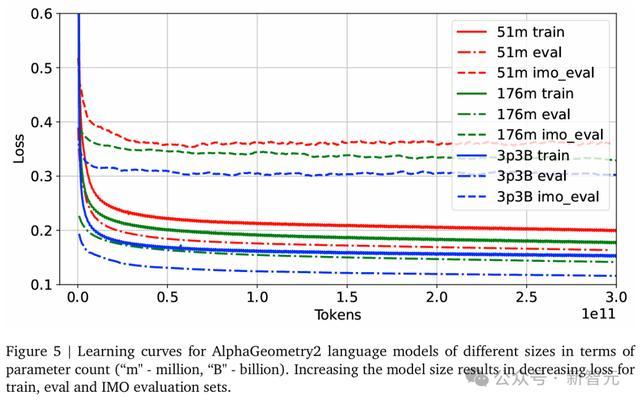
推理确立

在搜索算法方面，扣问东谈主员通过多个搜索树和不同限制的说话模子来搞定一个新的问题。

与AG1不同，扣问东谈主员使用了温度t=1.0和k=32的top-k采样。需要防卫的是，高温度和多个采样对于搞定IMO问题至关病笃。

在筹商解码模式下（即t=0.0，k=1，且不使用搜索树），模子只可搞定26个需要补助构造的问题中的2个。

而当温度提高到t=1.0并使用k=32个采样（但不使用搜索树）时，说话模子不错搞定26个问题中的9个。

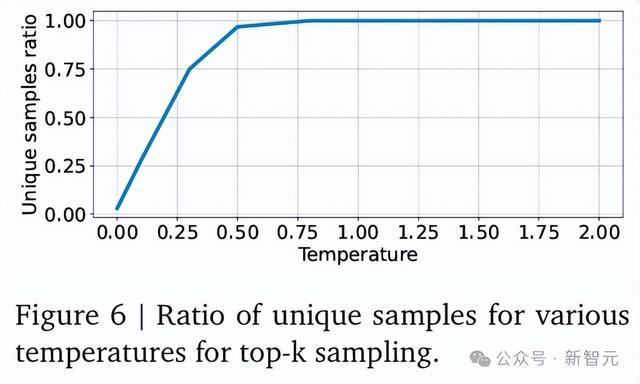
若是温度低于t=1.0，则生成的补助构造不够万般化（见图6）；而若是温渡过高，则会增多说话模子输出的虚伪范围说话语法的比例。

这个AI，泄露出超凡的创造力

谷歌团队中的几位几何群众和IMO奖牌得主仔细看过AlhpaGeometry的解题经过后，忍不住奖饰谈：它展示出了超凡的创造力！

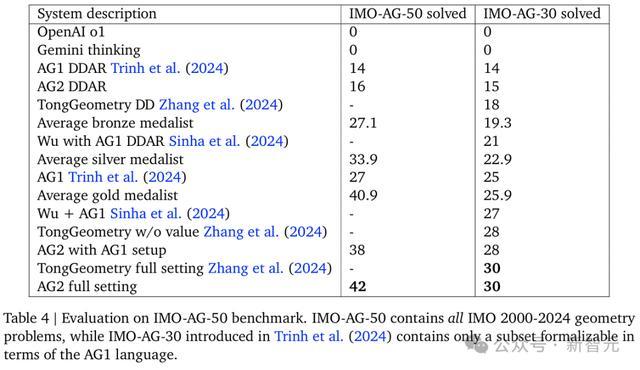
不同配置的AlphaGeometry2，以终点他系统的对比

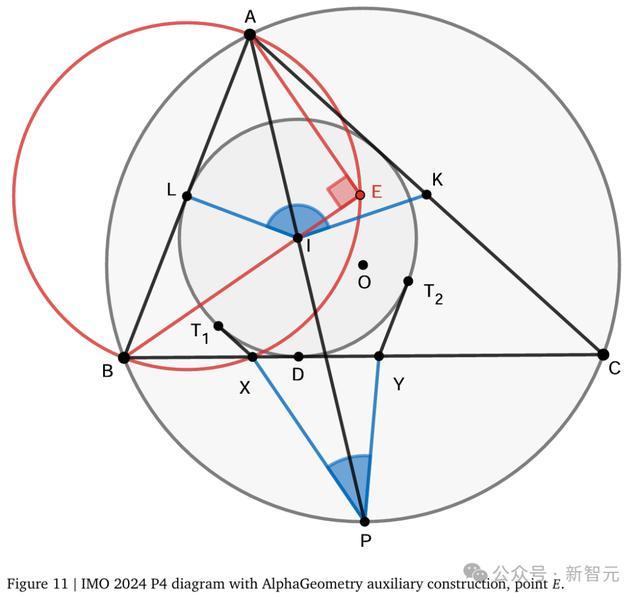
比如，底下这条题的∠KIL是由中点和内心酿成的角度，这两个几何元素频繁难以建筑关联，且无法径直通过主三角形ABC的角度来贪图。

在传统解法中，东谈主类参赛者频繁会借助三角函数、复数或其他贪图范例来求解。而对于AlphaGeometry而言，其DDAR系统仅依靠基本的角度干系推导和比例干系推导，因此需要引入一些补助点的构造。

为此，AlphaGeometry在直线BI上好意思妙地构造了点E，使得∠AEB = 90°。这一构造优雅地将那些看似无关的几何元素猜想起来，酿成了两对通常三角形：△ABE与△YBI、△ALE与△IPC。这些通常三角形产生了新的等角干系和等比干系，同期也揭示了点E与线段AB中点L之间的病笃猜想。

要完成施展，要道在于施展两组三角形的通常性：△AKI ∼ △BPY和△ALI ∼ △CPX，从而得出∠AIK = ∠BYP和∠AIL = ∠CPX。这还是过不错通过利用前述通常三角形所产生的边长比例干系来完成。

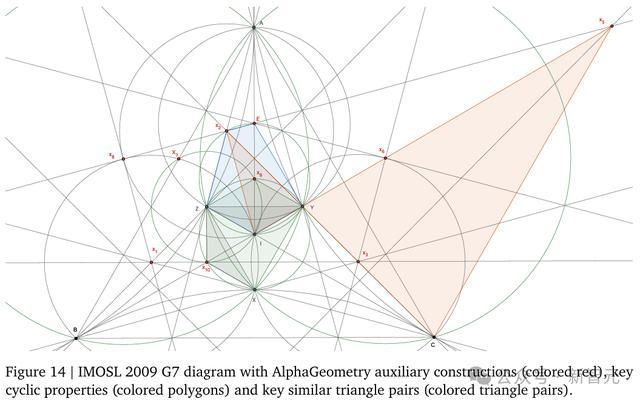
正如开篇所述，底下这谈题一直以来王人只好贪图性的解法，举例使用复数、三角贪图或通过不等式进行反证法。而AlphaGeometry既弗成使用这些贪图和推理用具，也不具备高档欧几里得几何学问。

然则，最终的截止却出乎预见——AlphaGeometry通过构建要道的补助作图，在只用角度和比例跟踪的情况下，给出了一个优雅的搞定决策。

率先，AlphaGeometry施展了X和Z对于BI对称，凭证对称性可知I是三角形XYZ的外心。由此不错施展AB = AC，凭证对称性可知三角形ABC是等边三角形。

然则，这个问题的主要挑战在于使用三角形XYZ是等边三角形的条目，即XY=YZ终点轮回变体。

为此，AlphaGeometry构造了一系列要道三角形的外心：

D是三角形BXC的外心

E是三角形AYZ的外心

X_1是三角形BIX的外心

X_2是三角形AIY的外心

X_3是三角形CIX的外心

X_4是三角形ABZ的外心

X_5是三角形ACY的外心

X_6是三角形AXZ的外心

X_7是I对于BZ的对称点

X_8是三角形AXY的外心

X_9、X_10是使得三角形IZX_9，三角形IZX_10为等边三角形的点

X_11是Z对于BI的对称点

发轫，这些构造看起来非常反直观，因为大多数东谈主不会构造这些点。沟通到点X,Y,Z的性质，这些点与通盘特定配置猜想的几何性质并未几，这使得东谈主类很难想出一个轮廓解法。

尽管如斯，这些外心构造有助于酿成非常/通常三角形对，这使得AlphaGeometry好像利用三角形XYZ是等边三角形这一事实来搞定问题。

从上头的例子中不错看到，AlphaGeometry在构造补助点方面非常高效，况且好像在不依赖复杂的欧几里得几何学问和用具的情况下，为难题提供非常优雅的搞定决策。这使得它好像产生东谈主类频繁无法猜度的，既富足创意又高效的解法。

那AlphaGeometry有哪些问题是尚未搞定的呢？

这么的问题有8个。

其中2个是它已尝试但未搞定的，而另外6个则是无法体式化的问题，比如触及到不等式和可变数目的点，这些当今还不在AlphaGeometry2说话的粉饰范围内。

另外2个则触及到了一些高档几何解法技能，如反演、投影几何或根轴等，这些技能在现时的DDAR中尚未杀青。

若是想要作念出这些题世博体育(中国)官方网站，就需要更长的推理时刻、更长的施展经过，以及更多的补助构造了，来弥补现频频间的不及了。